All published articles of this journal are available on ScienceDirect.
The Redefined First, Second and Third Zagreb Indices of Titania Nanotubes TiO2[m,n]
Abstract
The first and the second Zagreb indices are two of the most thoroughly studied and oldest topological indices. Recently in 2013, Ranjini et al. re-defined the Zagreb indices, i.e., the redefined first, second and third Zagreb indices of a graph G are defined as
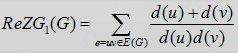 ,
,
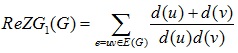 and
and
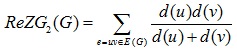 , respectively. In this research paper, we compute the redefined Zagreb indices of the Titania Nanotubes TiO2[m, n].
, respectively. In this research paper, we compute the redefined Zagreb indices of the Titania Nanotubes TiO2[m, n].
INTRODUCTION
Let G(V (G), E( G)) be a simple connected graph. In the setting of chemical graph theory, we use a graph G to model a chemical structures. Namely, we use the vertices and edges in G to represent respectively the atoms and the bonds in chemical structures. The vertex set and edge set of G are denoted by V (G) and E (G) respectively and for u, v ϵ V (G); e = uv is an edge of G(e ϵ E (G)). In a simple connected molecular graph G as order n, d(v) be the vertex degrees of vertices/atom v in G. Then 0 ≤ δ(G) ≤ d(v) ≤ Δ(G) ≤ n - 1, where δ(G) and Δ(G) are the minimum and maximum of degrees d(v) for all v ϵ V (G). The notations and terminologies that were used but were undefined in this paper can be found in [1, 2].
A topological index is a real number associated with a graph which characterizes the topology of the graph and is invariant under graph isomorphism. There are many distance or degree based topological indices. Degree based topological indices are of great importance and play a vital role in chemical graph theory. Some recent results on topological indices of chemical graphs have been studied by Gao et al. [3, 4].
The first and second Zagreb indices which were introduced by Gutman and Trinajstić [5] in 1972 are the oldest topological indices of graphs. They are degree based indices and expressed as follows:
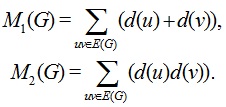 |
In 2012, Ghorbani and Azimi [6] proposed the multiple versions of Zagreb indices of a graph G. These new indices are first multiple Zagreb index PM1(G), second multiple Zagreb index PM2(G) and defined as:
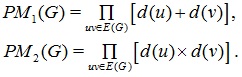 |
The reader can find more information about multiple versions of Zagreb indices of some molecular graphs and Nanotubes in [7-10].
In 2013, Shirdel et al. [11] introduced another degree based version of topological index named Hyper-Zagreb index and it is defined as:
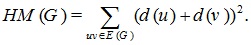 |
For more study about some properties of hyper Zagreb indices, see [12-16].
In 2004, Gutman and Das [17] defined the first and second Zagreb Polynomial in the following way:
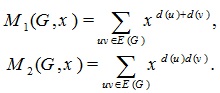 |
The properties of M1(G, x), M2(G, x) polynomials for some chemical structures have been studied in the literature [17, 18].
Ranjini et al. [19] re-defined the Zagreb indices, i.e. the redefined first, second and third Zagreb indices for a graph G and these are manifested as
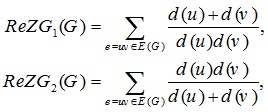 |
and
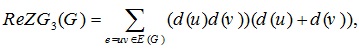 |
respectively.
MAIN RESULTS
Titania Nanotubes are studied comprehensively in materials science. Carbon nanotube composites have attracted much attention due to their unique properties and promising applications. Titanium dioxide (TiO2) is an important semiconductor material, and it has been applied as white pigment, cosmetic, catalyst and carrier owing to its excellent physical and chemical properties. The TiO2 sheets with a thickness of a few atomic layers were found to be remarkably stable [20-28]. The graph of the Titania Nanotubes TiO2[m, n] is presented in Fig. (1), where m denotes the number of octagons in a column and n denotes the number of octagons in a row of the Titania Nanotubes. Malik and Imran [25] computed the first and second Zagreb indices, first and second multiple Zagreb index for an infinite class of Titania Nanotubes TiO2[m, n].
In this paper, we computed the redefined Zagreb indices of Titania Nanotubes TiO2[m, n], for this initially we perform some necessary calculations.
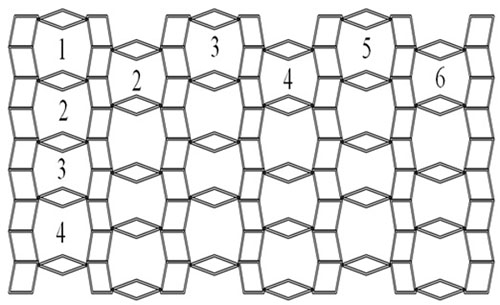
Let us define the partitions for the vertex set and edge set of Titania Nanotubes TiO2[m, n], for δ(G) ≤ a ≤ Δ(G), 2δ(G) ≤ b ≤ 2Δ(G) and δ(G)2 ≤ c ≤ Δ(G)2, then we have [25, 29, 30]:
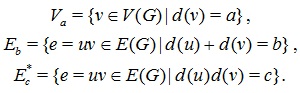 |
From [25, 29, 30], we can see that for all vertex/atom v in the molecular graph of TiO2 Nanotubes 2 ≤ d(v) ≤ 5, thus five vertex partitions of TiO2 with their cardinalities are as follows (see Table 1):
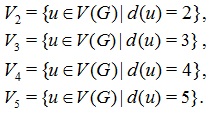 |
| Vertex partition | V2 | V3 | V4 | V5 |
| Cardinality | 2mn+4n | 2mn | 2n | 2mn |
The edge partitions of TiO2 Nanotubes with their cardinalities (see Table 2) are stated as follows.
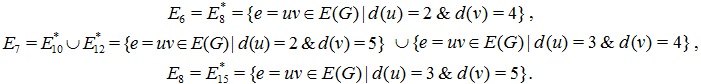 |
| Vertex partition | E6 = E8* | E7 | E8 = E15* | E10* | E12* |
| Cardinality | 6n | 4mn+4n | 6mn-2n | 4mn+2n | 2n |
For every vertex v ϵ V (G), d(v) belongs to exactly one class Va for 2 ≤ a ≤ 5 and for every edge uv ϵ E (G), d(u)+d(v) (resp. d(u)d(v)) belongs to exactly one class Eb (resp. Ec*) for 2δ(G) ≤ b ≤ 2Δ(G) and δ(G)2 ≤ c ≤ Δ(G)2. So, the vertex partitions Va and the edge partitions Eb and Ec* are collectively exhaustive, that is:
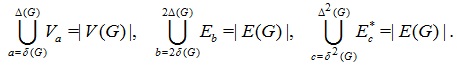 |
Now, we compute the redefined first, second and third Zagreb indices of Titania Nanotubes TiO2[m, n] in the following theorems.
Theorem 1: Let be the Titania Nanotubes, then the redefined first Zagreb indices is:
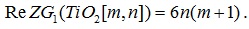 |
Proof. In terms of the definition of the revised first Zagreb index, we have:
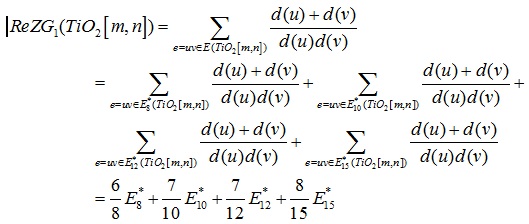 |
Form Table 2 we get:
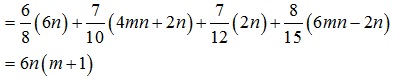 |
which is the required result.
Theorem 2. Let be the Titania Nanotubes, then the redefined second Zagreb indices is:
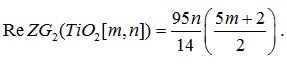 |
Proof. By means of the definition of the revised second Zagreb index, we infer:
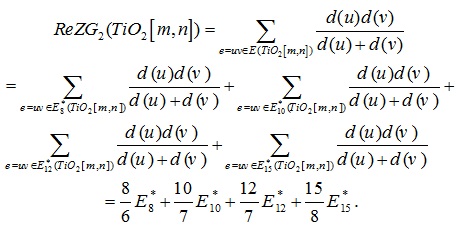 |
From Table 2 we deduce:
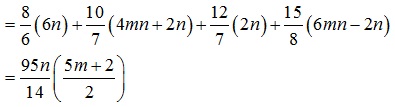 |
which is the expected result.
Theorem 3. Let TiO2[m, n] be the Titania Nanotubes, then the redefined third Zagreb indices is:
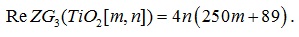 |
Proof. From the definition of revised third Zagreb index, we yield:
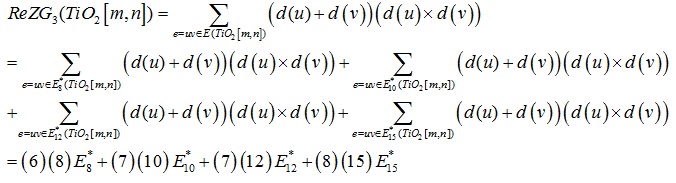 |
From Table 2 we obtain:
 |
which is the expected result.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
We thank the reviewers for their constructive comments in improving the quality of this paper. This work was supported in part by NSFC (11401519).


