All published articles of this journal are available on ScienceDirect.
Feature Selection Algorithm Based on Mutual Information and Lasso for Microarray Data
Abstract
With the development of microarray technology, massive microarray data is produced by gene expression experiments, and it provides a new approach for the study of human disease. Due to the characteristics of high dimensionality, much noise and data redundancy for microarray data, it is difficult to my knowledge from microarray data profoundly and accurately,and it also brings enormous difficulty for information genes selection. Therefore, a new feature selection algorithm for high dimensional microarray data is proposed in this paper, which mainly involves two steps. In the first step, mutual information method is used to calculate all genes, and according to the mutual information value, information genes is selected as candidate genes subset and irrelevant genes are filtered. In the second step, an improved method based on Lasso is used to select information genes from candidate genes subset, which aims to remove the redundant genes. Experimental results show that the proposed algorithm can select fewer genes, and it has better classification ability, stable performance and strong generalization ability. It is an effective genes feature selection algorithm.
1. INTRODUCTION
With the rapid development of microarray technology, massive microarray data is produced by experiments, which provides a new approach to study the disease. The dimensions of microarray data are higher, but the number of disease-related genes is fewer. The disease-related gene is called information gene. Feature selection technique is to select the subset of the relevant attributes from the high-dimensional data, which has been widely used in pattern recognition, artificial intelligence, data mining, machine learning and other fields [1], and is also an important tool to analyze the high-dimensional microarray data [2].
The sorting method is a simple and common method among information genes selection methods. The method scores all genes, then information gene are selected according to the scores. The more commonly used methods are mutual information method [3], Signal Noise Ratio method [4], Relief feature filtering algorithm [5] at present. However, genes selected by sorting method often have strong correlation, which result in redundant genes [6]. Too many redundant genes will make the scale of genes subset larger, increasing the computational burden, decreasing the distinguish ability, and resulting in classification errors. In order to remove redundant genes, Tan et al. [7] proposed different sorting methods to select genes subset; Wang Shulin et al. [8] proposed breadth-first search algorithm to select genes subset; Chuang et al. [9] proposed particle swarm algorithm and genetic algorithm to select genes subset; Yu et al. [10] proposed clustering algorithm to dynamically select genes subset; Benso A et al. [11] proposed spectral clustering to select genes subset; Chen et al. [12] proposed multi-core support vector machine to select genes subset. Above several algorithms remove redundant genes to some extent, but there may be over-fitting and poor generalization ability. Therefore, the design of a robust and efficient genes feature selection algorithm is the research focus of microarray data analysis.
Lasso method is a dimension reduction method based on linear regression model, which has attracted widespread attention in the field of feature selection because of its efficient performance [13]. If there is a strong correlation between genes, and they are mutually redundant, Lasso method may mistakenly take them as information genes. In addition, because linear regression model constructed by Lasso method is very strict, it is possible over-fitting exists. Therefore, we propose a new feature selection algorithm FSMIL (Feature Selection Algorithm based on Mutual Information and Lasso) to filter irrelevant genes and remove redundant genes. The algorithm is implemented by two steps; Step 1 uses mutual information method to filter irrelevant genes, and Step 2 uses an improved Lasso method to remove redundant genes. Experiments use 5 public microarray datasets to verify the feasibility and effectiveness of the algorithm.
2. FRAMEWORK OF FSMIL ALGORITHM
In order to select useful information genes from high-dimensional microarray data, filter unrelevant genes and remove redundant genes, we propose a new feature selection algorithm based on mutual information and Lasso FSMIL, and its framework is shown in Fig. (1). The algorithm is implemented by two steps; Step 1 uses mutual information method to filter irrelevant genes, and Step 2 uses an improved Lasso method to remove redundant genes.
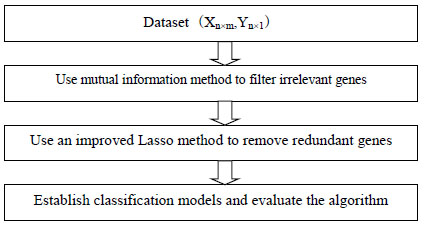
Assuming that there are n samples, m genes in microarray dataset (X, Y), the detailed steps of the algorithm are as follows:
- Use mutual information to calculate the values of m genes, and select m' higher value genes.
- Use an improved Lasso method to select m” genes from m' genes.
- Establish classification models and evaluate the performance of the algorithm.
(1) and (2) will be discussed in detail later. In (3), we use several different classification models and LOOCV method to evaluate the performance of the algorithm. LOOCV method is a special kind of cross-validation method that is used commonly. Every time it selects a sample as test sample, the remaining samples are used to establish classification model.
3. MAIN TITLE MUTUAL INFORMATION METHOD
In general, the dimensions of microarray data are very higher, but the number of disease-related genes is fewer. Therefore, there are a large number of irrelevant genes in microarray data, which are not much affected and sometimes cause interference in diagnosing the disease.
Mutual information is the index measuring the correlation between the two variables, which is one of the most effective filtration methods as it is simple and efficient. In the process of selecting genes, mutual information value is used to measures the correlation between gene and classification category. If the mutual information value is larger, it means more classification information is in genes, and its importance is also higher. Mutual information value is calculated by entropy and conditional entropy. Assuming that X and Y represent gene and category, x and y represent the value of the corresponding X and Y respectively, p(x) and p(y) represent the probability of gene X and gene Y respectively, p(xy) is the joint probability of X and Y, p(x|y) is the conditional probability of X. The mutual information MI (X,Y) is calculated as follows:
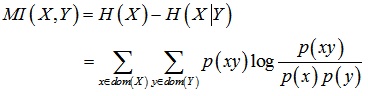 |
(1) |
where p(x) and p(y) represent the probability of gene X and gene Y respectively, p(xy) is the joint probability of X and Y.
Information entropy H(X) is:
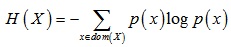 |
(2) |
Conditional entropy H(X|Y) is:
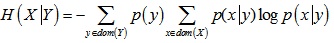 |
(3) |
where p(x|y) is the conditional probability of X.
For continuous attribute data, we firstly deal with continuous data into discrete data, and then calculate the mutual information. The detailed steps that we filter irrelevant genes are: firstly the mutual information value of m genes is calculated according to formula (1), then all genes are sorted by the mutual information value in descending order, and the first m' genes are selected as a candidate genes subset, usually m '<< m. However, the m' genes are usually strong relevant, it will result in redundancy. If redundancy genes are too many, the candidate genes subset will become larger, which increase the computational burden and decrease the distinguish ability. Therefore, we use an improved Lasso method to remove redundant genes, get m” information genes from m' genes.
4. IMPROVED LASSO METHOD
Lasso method is originally proposed to describe the optimization problem with constraints by the scholar Tibshirani [14], which is widely used in microarray data analysis because of its simplicity and efficiency. The basic idea of the algorithm is that when the sum of the absolute value of the regression coefficients is less than the threshold, the minimum sum of residuals square is calculated, that will cause that the value of some regression coefficients is equal to 0. Assuming the data (X, Y) containing n samples with m features, X = (x1, ..., xj, ..., xm), xj = (x1j, x2j, ..., xnj) T is the independent variable; Y = (y1, ..., yi, ..., yn) T, yi is the response variable, i = 1,2, ..., n; j = 1,2, ..., m. Under the condition that the 1-norm of regression coefficients β = (β1, β2, ..., βm) is less than the threshold t, the data (X, Y) is analyzed by linear regression.
Standardized on xj, and centered on yi:
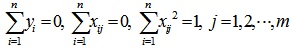 |
(4) |
Minimize the sum of residuals square:
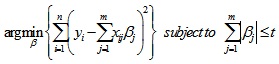 |
(5) |
In the formula (5), the threshold t can be adjusted. When the threshold t is set relatively small, regression coefficients that the correlation is not high and will be reduced to 0. Removing these variables whose regression coefficient is 0 can implement feature selection. When the threshold t is set relatively large, the constraint conditions will no longer work, and all attributes will be selected as features.
The correlation between genes in candidate genes subset selected by mutual information method is generally strong. If these genes are also mutually redundant and features are directly selected by Lasso method, these genes will be mistaken as information genes. Therefore, in order to effectively remove redundant genes and overcome the lack of Lasso method, we propose an improved Lasso method to remove redundant genes. The detailed implementation process is as follows: (X, Y) is a training set after filtering irrelevant genes; Genes in Glist are sorted by the mutual information value in ascending order, and sequentially generates K genes subsets, denoted Glist (i). Firstly initializing that information genes subset Sbest is empty, then add current information genes subset Sbest into Glist (i) as a new genes subset; The features of data subset Xi that is corresponding to new genes subset Glist (i) are selected by the improved Lasso method to remove redundant genes and retain information genes; Finally the optimal information genes subset Sbest is obtained after K times iterations.
Assuming that Gi, Gj are information genes strongly correlated with the classification category, and Gi (Gj) is a redundant gene of Gj (Gi). If features are directly selected by Lasso method, Gi and Gj are more likely retained as information genes. If features are selected by the improved Lasso method, in the process of filtering irrelevant genes in step 1 Gi and Gj are selected as information genes, but when features are selected second time by the improved Lasso method in step 2, since the algorithm uses iterative strategy, regardless of whether Gi and Gj are distributed into the same genes subset originally, genes will be iteratively selected next time. After iterations many times, redundant genes can be effectively removed. Therefore, the improved Lasso method proposed in the paper can remove redundant genes to some extent. Its detailed implementation steps are shown in Fig. (2).

5. EXPERIMENTAL RESULTS AND ANALYSIS
5.1. Experimental Datasets and Environment Configuration
Experiments use 5 public microarray datasets to evaluate the performance of the algorithm proposed in this paper. The detailed description of the datasets is shown in Table 1.
| ID | Name | Genes number | Samples number (positive/negative) |
Categories number |
|---|---|---|---|---|
| 1 | Colon | 2000 | 62 (40/22) | 2 |
| 2 | Prostate | 12600 | 102 (52/50) | 2 |
| 3 | Lymphoma | 7129 | 77 (58/19) | 2 |
| 4 | Leukemia | 7129 | 72 (25/47) | 2 |
| 5 | Lung | 12533 | 181 (31/150) | 2 |
- Colon dataset: The dataset contains 62 samples, including among them 40 colon cancer samples and 22 normal samples; each sample is composed of 2000 genes.
- Prostate dataset: The dataset contains 102 samples, including 52 prostate cancer samples and 50 normal samples; each sample is composed of 12,600 genes.
- Lymphoma dataset: The dataset contains 77 samples, including 58 diffuse large B-cell lymphoma samples, 19 follicular lymphoid tumor samples; each sample is composed of 7129 genes.
- Leukemia dataset: The dataset contains 72 samples, including 25 acute myeloid leukemia samples and 47 acute lymphoblastic leukemia samples; each sample is composed of 7129 genes.
- Lung datasets: The dataset contains 181 samples, including 31 malignant pleural mesothelioma samples and 150 malignant breast cancer samples; each sample is composed of 12533 genes.
In this paper, experimental environment is configured as follows: Intel CPU 3.40 GHZ, 4GB memory, the PC, Windows 7 operating system, Weka + Matlab development environment. We uses 4 classification models, namely support vector machine SVM, K neighbors KNN, C4.5 decision tree and random forest. The kernel function of SVM is configured to polynomial kernel function, the neighbor number of KNN is configured to 10, the confidence factor of C4.5 for pruning is configured to 0.25, and the tree number of random forest is configured to 10.
5.2. Analysis of Experimental Results
The proposed algorithm in this paper firstly uses mutual information method to select m' genes from m genes in order to filter irrelevant genes; then uses an improved Lasso method to select m” genes from m' genes in order to remove redundant genes. Therefore, the experiment will study from the following 3 aspects.
5.2.1. Experimental Analysis of Mutual Information Method
Generally in the range of genes number is Top 50-200 selected by mutual information method, this paper selects 100 genes as candidate genes subset. In order to test the performance of candidate genes subset selected by mutual information method, the experiment firstly uses mutual information method to select 100 information genes on 5 microarray datasets, then uses 4 different classification models to classify, and the average classification accuracy is as the final classification accuracy Acc. The experiment also directly uses 4 different classification models to classify the original datasets. The experimental results of the original datasets and the datasets selected by mutual information method are shown in Table 2, Genes represents the genes number, Acc represents the average classification accuracy.
| Dataset | Original genes set | Candidate genes subset | ||
|---|---|---|---|---|
| Genes | Acc(%) | Genes | Acc(%) | |
| Colon | 2000 | 82.28 | 100 | 86.44 |
| Prostate | 12206 | 84.82 | 100 | 92.59 |
| Lymphoma | 7129 | 91.27 | 100 | 94.64 |
| Leukemia | 7129 | 86.77 | 100 | 93.10 |
| Lung | 12412 | 95.19 | 100 | 98.08 |
As can be seen from Table 2, the classification accuracy of the candidate genes subset selected by the mutual information method is no less than the classification accuracy of the original dataset. This shows that most of the genes filtered by the mutual information method are irrelevant genes and the retained genes are information genes. Experimental results show that Top 100 genes can achieve more accurate classification on the original genes dataset, which contain the complete classification information of the original genes dataset.
5.2.2. Experimental Analysis of Improved Lasso Method
In order to verify the performance of the improved Lasso method removing redundant genes, experimental analysis of Lasso method and the improved Lasso method is done.
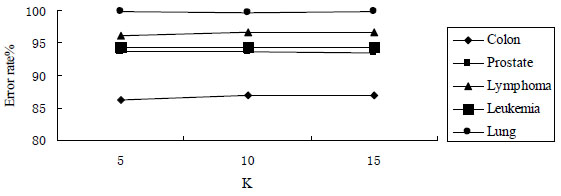
Because genes dataset is divided into K parts by the improved Lasso method, the value of the parameter K needs to be determined before the experiment. When the values of the K are different, the experiments on 5 public microarray datasets is done, and classification accuracy Acc is the average classification accuracy obtained by 4 different classification models. The experimental results are shown in Fig. (3). As can be seen from Fig. (3), when the value of K changes, classification accuracy obtained by the improved Lasso is no great change, which shows the improved Lasso method is not sensitive to the value of K. In order to select the relatively better value of K, we analyze the value of K. The value of K can not be too large. The large value of K means more divided parts, thus the number of genes of each part is relatively less. The value of K can not be too small. The small value of K means less divided parts, thus the number of genes of each part is relatively more. The both cases are unfavorable to select information genes.
Here we verify the performance of the improved Lasso method removing redundant genes. In the experiment, the candidate genes subset obtained by mutual information method is classified by Lasso method and the improved Lasso method; the optimal solution of Lasso method is obtained by least angle regression algorithm. The genes number of candidate genes subset is Top 100, and the value of K is 10, which is perfect in the experiment above. The genes number Genes and the average classification accuracy Acc are shown in Table 3.
| Dataset | Lasso | Improved Lasso | ||
|---|---|---|---|---|
| Genes | Acc(%) | Genes | Acc(%) | |
| Colon | 6 | 86.49 | 4 | 86.86 |
| Prostate | 61 | 93.16 | 8 | 93.61 |
| Lymphoma | 11 | 95.92 | 10 | 96.56 |
| Leukemia | 24 | 93.69 | 15 | 94.36 |
| Lung | 9 | 98.55 | 7 | 99.60 |
As can be seen from Table 3, the number of information genes and classification accuracy of the improved Lasso method are superior to Lasso method on 5 public microarray datasets. For example, on Prostate dataset the number of information genes selected by Lasso method is 62, however, the number of information genes selected by the improved Lasso method is only 16, which greatly reduces the dimensions of genes. Meanwhile, the classification accuracy of the improved Lasso method is also not less than the Lasso method. Therefore, the improved Lasso method can effectively remove redundant genes.
5.2.3. Experimental Analysis of FSMIL Algorithm
Finally, in order to verify the performance of FSMIL algorithm, 5 public microarray datasets are classified by FSMIL algorithm, meanwhile, it is compared with the classic mutual information method and Lasso method. Firstly, FSMIL algorithm uses mutual information method to calculate the value of mutual information for all m genes, and select the Top 100 (m '= 100) genes as a candidate genes subset according to the mutual information value in descending order; then uses the improved Lasso method to select information genes from candidate genes subset. The parameter K is set to 10, which is perfect in the experiment above. In order to compare with FSMIL algorithm, the number of genes selected by mutual information method is also set to 100. Firstly SVM is adopted as classification model. The classification results of SVM on information genes subsets selected by 3 feature selection method and the original dataset are shown in Table 4.
| Dataset | Original | MI | Lasso | FSMIL |
|---|---|---|---|---|
| Colon | 87.21 | 90.42 | 90.45 | 90.86 |
| Prostate | 91.12 | 96.34 | 96.38 | 96.52 |
| Lymphoma | 98.63 | 97.52 | 97.54 | 98.68 |
| Leukemia | 98.39 | 98.41 | 98.42 | 98.63 |
| Lung | 99.52 | 99.53 | 99.57 | 100 |
Table 4 shows the classification performance of SVM on 5 public microarray datasets. The “original” column represents the classification accuracy of SVM on the original microarray dataset, which does not use any feature selection algorithm and directly uses SVM. “MI”, “Lasso” and “FSMIL” 3 columns represent the classification accuracy of SVM on the information genes subsets selected by 3 different feature selection algorithms. As can be seen from Table 4, the classification accuracy of the proposed feature selection algorithm on 5 public microarray datasets is not less than other algorithms, which shows FSMIL method retains the useful genes of the original dataset, filters irrelevant genes and removes redundancy genes.
To confirm whether the proposed algorithm FSMIL in other classification models still has good classification performance, it also uses the KNN, C4.5 and random forest 4 classification models on 5 public microarray datasets to experiment. The experimental results are shown in Tables 5-7. As can be seen from Table 5, the classification accuracy of FSMIL algorithm on 5 microarray datasets is not less than KNN classification model on the original microarray datasets, and also better than KNN classification model on the information genes subsets selected by other feature selection algorithms. As can be seen from Table 6, the classification accuracy of FSMIL algorithm in Colon dataset is slightly lower than C4.5 classification model in the original microarray dataset, but the absolute value of the difference between them is only 1.61%. The average accuracy of FSMIL on 5 experimental datasets is the highest. The number of information genes selected by FSMIL is fewer, only 4 dimensions, is not helpful to establish decision tree model, so the classification accuracy is lower than the “original” column and the “MI” column the number of information genes of which is 100. As can be seen from Table 7, the classification accuracy of FSMIL algorithm on 5 microarray datasets is not less than the random forest classification model on the original microarray dataset, and also better than the random forest classification model on the information genes subsets selected by other feature selection algorithms.
| Dataset | Original | MI | Lasso | FSMIL |
|---|---|---|---|---|
| Colon | 78.43 | 88.87 | 88.89 | 88.92 |
| Prostate | 76.57 | 93.31 | 94.75 | 96.13 |
| Lymphoma | 88.12 | 94.53 | 98.54 | 98.58 |
| Leukemia | 78.68 | 97.41 | 98.36 | 98.64 |
| Lung | 92.35 | 100 | 99.48 | 100 |
From the experimental analysis of the above 3 aspects, the number of information genes selected by FSMIL algorithm is fewer, which are not more than 16 dimensions, and even the minimum number reaches 9 dimensions. However, FSMIL algorithm on the overall classification accuracy is not less than other algorithms, which shows FSMIL algorithm can select information genes, filter irrelevant genes and remove redundancy genes to some extent. Therefore, FSMIL algorithm can select fewer information genes, and it has better classification ability, stable performance and strong generalization ability. It is an effective genes feature selection algorithm to solve the high dimension and high redundancy problems of microarray data.
| Dataset | Original | MI | Lasso | FSMIL |
|---|---|---|---|---|
| Colon | 82.74 | 82.92 | 81.13 | 81.13 |
| Prostate | 87.14 | 87.85 | 88.38 | 88.46 |
| Lymphoma | 88.47 | 90.76 | 91.21 | 92.53 |
| Leukemia | 80.76 | 81.94 | 82.57 | 84.32 |
| Lung | 96.23 | 96.45 | 98.91 | 98.94 |
| Dataset | Original | MI | Lasso | FSMIL |
|---|---|---|---|---|
| Colon | 80.75 | 83.56 | 85.47 | 86.52 |
| Prostate | 84.46 | 92.85 | 93.12 | 93.31 |
| Lymphoma | 89.87 | 95.74 | 96.38 | 96.43 |
| Leukemia | 89.23 | 94.64 | 95.41 | 95.85 |
| Lung | 92.65 | 96.32 | 96.24 | 99.46 |
CONCLUSION
Microarray data has a very important role for diagnosis of the disease, however, high dimension and high redundancy of microarray data brings great difficulties for mining knowledge from microarray data profoundly and accurately, and information genes selection is a very critical task. In this paper, a new feature selection algorithm FSMIL is proposed, which takes microarray datasets as specific study objects. The algorithm is implemented by2 steps; Step 1 uses mutual information method to calculate the mutual information value of all genes, and selection information genes according to the mutual information value in descending order to filter irrelevant genes and remove redundant genes. Step 2 uses the improved Lasso method to select candidate genes subset to remove redundant genes. Experimental results show that the algorithm can select the fewer genes, and it has better classification ability, stable performance and strong generalization ability to solve high dimension and high redundancy problems of microarray data. It is an effective information genes feature selection algorithm.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The work was jointly supported by the National Natural Science Foundation of China and Shenhua Group Co., Ltd. (51174257/E0422), and supported by “the Fundamental Research Funds for the Central Universities of Hefei University of Technology(2013bhzx0040), and supported by the Natural Science Foundation of the Anhui Higher Education Institutions of China (KJ2016A549), and supported by the Natural Science Foundation of Fuyang Teachers College (2016FSKJ17).


