Non-Resonant Frequencies of Electromagnetic Fields in α-Helices Cellular Membrane Channels
RESEARCH ARTICLE

Non-Resonant Frequencies of Electromagnetic Fields in α-Helices Cellular Membrane Channels

Emanuele Calabrò1 , 5 , * Open Modal Salvatore Magazù1 , 2 , 3 , 4
Authors Info & Affiliations
The Open Biotechnology Journal • 31 May 2018 • RESEARCH ARTICLE • DOI: 10.2174/1874070701812010086

Abstract

Background:

This paper would be a starting point addressed to a methodology to minimize the effects on livings of man made Electromagnetic Fields (EMFs) pollution.

Methods:

Given that previous literature highlighted that the most relevant EMFs effects on biological systems can be due to resonance phenomena between electromagnetic field and organic matter, it was proposed here an algorithm to obtain values of frequencies of an applied electromagnetic field far from resonant frequencies, depending on the natural frequencies and viscous damper of a biological system. These frequencies have been named non-resonant frequencies.

Results:

The displacement of the α-helices in cellular membrane channels due to EMFs has been proposed as a relevant parameter for quantifying the result of the interaction between an applied EMF and organic matter, in order to find both the natural frequencies of a biological system and the resonant frequencies at which α-helices displacement should be maximum.

Conclusion:

The non-resonant frequencies can be obtained using the algorithm proposed here.

Keywords: Electromagnetic field, Resonance, α-helix, Biological systems, Cellular membrane channels, Non-resonant frequencies, Natural frequencies.

1. INTRODUCTION

The development of modern technology has induced an enormous increasing of the use of electric power devices working at electromagnetic fields frequencies at 50 or 60 Hz (named Extremely Low Frequencies Electromagnetic Fields – ELF-EMFs) and of broadcasting and mobile stations working at High Frequencies Electromagnetic Fields (HF-EMFs) up to a few GHz.

Regarding harmfulness to human health of EMFs a very large scientific production has been published by single researchers and some valuable studies have been published also by international working groups [1-6]. Some relevant health effects that have been highlighted in [1-6] are neurodegenerative and cardiovascular disorders, alterations of immune system responses and reproduction in animals and in humans, genotoxic effects, increasing of global incidence of breast cancer, childhood leukaemia and general carcinogens.

The amount of these results has induced the International Commission on Non-Ionizing Radiation Protection (ICNIRP) to publish international guidelines in order to identify exposure limits of EMFs that are recommended not to be exceeded [7-11].

Nevertheless, recent studies have showed that significant effects occur in simple organic systems even below the EMFs limits recommended by the ICNIRP [12-24]. In particular, these studies showed that significant transitions from proteins α-helix component to β-sheet structure (that represents proteins unfolding) and orientation towards the direction of the applied field occur under exposure to EMFs below the limits recommended by the ICNIRP.

Proteins unfolding is responsible for aggregation mechanisms, so that previous results lead us to hypothesize that EMFs can be a cofactor for some diseases. Indeed, proteins aggregation can be considered the precursor of various neurological disorders such as Alzheirmer, Parkinson and Huntington, because proteins aggregation in the fibrillar form (the amyloid) can be associated with signs of neurodegeneration and some forms of anemia [25-33].

Some studies showed that some bioprotectors can induce shielding action against exposure to EMFs [34-39]. Nevertheless, we do not know what may be the side effects in humans living functions of a continuous use of such bioprotectors.

However, previous studies hypothesized that natural frequencies in livings could be close to the frequencies of man-made EMFs, so that a resonance phenomenon could occur amplifying the result of the interaction mechanisms between EMFs and organic matter [40-48]. Following this scenario, this study starts from the assumption that, similar to the existence of frequencies at which a resonance phenomenon between EMFs and organic matter occurs, there may be frequency regions with an opposite effect to that of resonance, in which the effects of interaction between EMFs and organic matter are minimal. We have named such frequencies ‘non-resonant frequencies’. In order to hypothesize to plan electronic devices working at such frequencies, this study proposed an algorithm to calculate the non-resonant frequencies of EMFs as a function of natural frequencies of organic matter. In particular, the displacement of α-helix in cellular membrane channels due to the interaction with EMFs has been proposed as a parameter useful to quantify harmful effects of EMFs on livings, given that it was shown that the orientation of α-helices in cellular membrane channels along the direction of the applied field should induce an increase of ions flux across the channel, changing cellular functions [24]. The existence of α-helix structure in proteins was proposed in 1951 by Linus Pauling and its existence was confirmed by X-ray crystallography. The α-helix consists of 3.6 amino-acid residues per turn in the polypeptide chain which is stabilized by hydrogen bonding between the amide hydrogen of one peptide bond and the carbonyl oxygen of another. The α-helix structure has a fundamental role in livings because it is present in all types of biological membranes [49-51].

The aim of this study was to propose an algorithm to find the non-resonant frequencies at which α-helices displacement be minimum, in order to minimize the effects of EMFs on livings as it is explained in the next sections.

2. METHODS

2.1. The Non-Resonant Frequencies Algorithm

Resonance is a phenomenon represented by the oscillation at high amplitude of a material, which occurs when the material is subjected to an external forcing at a specific frequency known as resonant frequency. When the frequency of the external forcing is close to a natural frequency of the material, a large vibration of the system is produced giving rise to the phenomenon named resonance.

Generally, a material has more than one resonant frequency. Each substance has some natural vibration frequencies that are characteristic of the material, depending on the frequencies of free vibrations of the molecules forming the material. The fundamental frequency is the lowest natural frequency, which gives rise to the maximum-amplitude oscillation of the system if it is stressed by an external forcing at that frequency. The frequencies at which a material will vibrate with large amplitude if it is forced are the natural frequencies of the material.

In contrast, if the system will be exposed to frequencies very different from its resonant frequencies, the system would not vibrate significantly.

Obviously, also biological systems are expected to have resonance frequencies in some regions of the electromagnetic spectrum. In particular, in previous literature it was proposed that biological systems can exhibit natural resonant frequencies in the microwave region [40, 52-56].

First, in order to study the interaction between EMFs and organic matter, an appropriate model has to be chosen to represent the response of biological systems to EMFs.

However, given that a biological system is a complex system, it would be represented by a large number of natural frequencies that cannot all be taken into account. Thus, we focused on cellular membrane channels α-helices, because their displacement due to EMFs should change the delicate equilibrium of ions flux across cells membrane channels [21, 24].

The α-helix behavior in cellular membrane channels in response to an applied EMF can be described by a viscoelastic model by means of three parameters, the spring, damper and mass elements. The modeling by a viscoelastic model of a generic organic system under an applied EMF was already proposed by [57, 58].

The external force acting on a charged particle can be represented by the term qE, in which q is the charge of the organic system and E is the electric field component of the EMF, which can be expressed by a sinusoidal function:

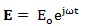(1)

Generally, this term is correlated to the magnetic component by Maxwell’s equations. Nevertheless, it was shown that the far-field approximation can be applied to the EMF emitted by wireless devices at working distance, whose the most representative is mobile phone [59]. In this case, the electric and magnetic field components are closely related as the ratio of the electric field to the magnetic field component is given by:

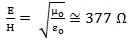(2)

where μ o and ε o are the permeability and permittivity of free space, respectively, so that it is sufficient to evaluate only one of them.

Furthermore, given that the organic system exposed to EMF should have non-negligible dimension, the torque induced by the EMF on the system has to be taken into account. In addition, it has to be compared to the Brownian motion due to thermal agitation, to which the organic system embedded in aqueous environment is subjected. To this aim, the angular impulse from EMF, that is ΔE*μ, should be compared with the mean angular momentum from thermal agitation 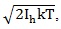, in which Ih is the moment of inertia of the organic system. Adair performed a simulation using hemoglobin as a typical simple organic system [60], providing the result that the mean angular momentum from thermal agitation is larger than the impulse from an applied electric field with amplitude E=100 kV/m. Nevertheless, the simulation of [60] can be applied to a dipole exposed to a EMF in the vacuum. In contrast typical organic systems such as cells or proteins α-helices can be considered macrodipoles embedded in a aqueous medium whose viscosity cannot be neglected, so that they cannot follow the oscillation of the applied HF-EMF due to the inertia of molecules and the viscosity of the medium, placing theirself at an average position along the direction of the field [24]. However, recently it was shown that 3 h exposure to EMFs of hemoglobin in aqueous solution samples induces that the impulse from the magnetic field overheads the mean angular momentum from thermal agitation [61]. The term due to thermal molecular agitation represents the viscosity of the medium in which the organic system is embedded can be taken into account by the damper coefficient of the medium ν.

Finally, the equation of motion of this viscoelastic model which can represent the behavior of the organic system exposed to EMFs is represented by the following equation:

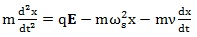(3)

in which m is the mass of the system, ν is the damper coefficient, k is the spring element of the system and ωs is a fundamental frequency of the system. In addition, 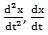and x are, respectively, the acceleration, velocity and complex displacement of a particle which is subjected to the applied electric field.

The generic solution of Eq. (3) is as follows:

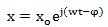(4)

where x o and φ are the amplitude of displacement and the phase angle, respectively, that are to be calculated. Let we consider that the oscillation of the system begins with beginning of exposure to the external field, so that it is φ = 0. Hence, we may rewrite the Eq. (4) as follows:

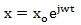(5)

The corresponding velocity and acceleration of the charged particle are, respectively,

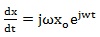(6)
(7)

Solving Eq. (3) for the displacement, putting x = x o for simplicity, we get:

(8)

A resonance phenomenon occurs when the frequency of the applied field is close to a fundamental frequency of the system ω = ωs, giving the maximum value of displacement x which is provided by Eq. (8).

Rationalizing the denominator of Eq. (8) where the imaginary unit appears, the Eq. (8) can be written as follows:

(9)

The algorithm proposed here is based on the assumption that values of frequencies ω that minimize the displacement of a charged particle in Eq. (9) exist and can be found using the mathematical condition that the first derivative of Eq. (9) is equal to zero:

(10)

This mathematical condition is expressed by the following equation:

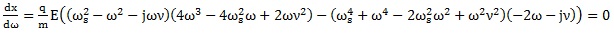(11)

Solving the Eq. (11) with respect to the frequency ω of the applied electric field we get:

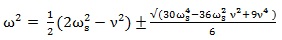(12)

The frequency values ω can be obtained by Eq. (12) as a function of the natural frequency ωs and of the damper coefficient values of an organic system. These frequency values ω should minimize the displacement x of charged particles exposed to an applied electric or magnetic field and can be named non-resonant frequencies. This procedure can be easily extended to an applied HF-EMF.

In conclusion, it was shown that given an EMF acting on an organic system, the smallest displacement of the organic charged particles exposed to the field can be found at particular frequencies of the applied EMF, that are correlated to the natural frequency and damper coefficient of an organic system.

2.2. Applying the Non-Resonant Frequencies Algorithm

Given that Eq. (12) can provide the non-resonating frequencies in any biological system as a function of natural frequency ωs and damper coefficient ν, the problem seems to be easily solved by knowing these values.

Nevertheless, the greatest difficulty is just knowing the natural frequencies ωs and damper coefficient ν in an organic system.

Previous literature provided some values of natural frequencies in some organic systems. For instance, some authors proposed the possibility that biological systems can exhibit natural frequencies in the MWs frequencies range [43-48, 52-58, 62]. [63] proposed resonance frequencies at 41.3 and 51.7 GHz for the bacterium Escherichia coli.

Nevertheless, a biological system is very complex system so that its natural frequencies cannot be easily found. In order to find these frequencies, we can choose one of the most representative parameters of a biological system whose interaction with an applied EMF gives rise to the maximum change in the livings functions of the organism.

3. RESULTS

In our opinion, this physical-chemical parameter which has a fundamental role in the resonance phenomenon with an applied EMF can be the flux of ions across cellular membranes, because its alteration changes the delicate equilibrium inside the cell altering cell viability. Indeed, ion channels in cellular membranes have been demonstrated to have a fundamental role in cellular functions [64-67].

In this regard, the displacement of α-helices in cells membranes channels caused by resonant frequencies of an EMF should alter the flux of ions across the channels, inducing damaging of cells [24]. In contrast, the application of an EMF with non-resonant frequencies should induce lesser α-helices displacements than an EMF with resonant frequencies.

In this scenario, the resonant frequencies in cellular membrane channels can be found measuring the displacement of the α-helices in membranes channels as a function of the frequency of an applied EMF, following the protocol accurately described in [13, 15]. For instance, Circular Dichroism (CD) spectroscopy can be used to measure the shift of the alpha helix with respect to its resting position in the cellular membrane channels as a function of the frequency of an applied EMF. CD is a spectroscopic technique which is generally used to study the secondary structure of proteins and in particular of membrane proteins [68]. However, this technique may be coupled with more sophisticated techniques such as X-ray crystallography or NMR spectroscopy. CD spectroscopy has the advantages of exploring a wide range of solution conditions and the rapid data collection. Other useful techniques to determine the orientation of proteins α-helices is the Nonlinear Sum Frequency Generation Vibrational (NSFGV) spectroscopy which can be coupled with linear vibrational spectroscopic techniques such as infrared spectroscopy and Raman scattering [69]. In previous studies measurements of α-helices tilt orientation have been carried out using CD spectroscopy, NMR and fluorescence spectroscopy and are reported in [70-72], respectively, showing that α-helices tilt orientation can be easily measured before and after exposure to EMFs in any type of tissue. In addition, it was already shown in [21, 24] that the orientation of cellular membrane channels α-helices along the direction of the applied EMF should cause the enlargement of cellular membrane channels, inducing the increasing of ions flux across cells channels and changing cellular functions.

Once the values of the natural frequencies at which the displacement of the α-helices in cellular membranes channels is maximum have been found, the values of the non-resonant frequencies can be obtained by Eq. (12) and using damper coefficient values such as proposed in [73-77].

CONCLUSION

Given the numerous evidence on the harmful effects of EMFs on livings, a strategy to reduce human exposure to EMFs was investigated. Considering that it has been highlighted in previous literature that a resonance phenomenon can occur whenever the frequency of the EMF is close to the natural frequency of the biological system invested by an electromagnetic radiation, an algorithm has been proposed here in order to obtain frequencies far from the natural frequencies of a biological system.

To this aim, the displacement of α-helices in cellular membrane channels has been proposed as a parameter aimed to measure the intensity of the interaction between EMF and organic matter, in order to find the biological natural frequencies that have the most important role in cellular functions of livings.

Once such natural frequencies have been found in typical organic tissues by measurements described at the end of previous section, non-resonant frequencies can be obtained using the algorithm here proposed, in order to hypothesize to plan electronic devices working at such frequencies, minimizing harmful effects of EMFs on livings.

ETHICS APPROVAL AND CONSENT TO PARTICIPATE

Not applicable.

HUMAN AND ANIMAL RIGHTS

No animals/humans were used for studies that are the basis of this research.

CONSENT FOR PUBLICATION

Not applicable.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.

ACKNOWLEDGEMENTS

Declared none.

REFERENCES

1
WHO. (World Health Organization) Extremely low frequency (ELF) fields Environmental Health Criteria 1984; Vol. 35 ISBN 92-4-154095-8.
2
WHO. (World Health Organization) Magnetic fields Environmental Health Criteria 1987; Vol. 69
3
(World Health Organization) Electromagnetic fields (300 Hz to 300 GHz) Environmental Health Criteria 1993; Vol. 137
4
IARC. Working Group on the Evaluation of Carcinogenic Risks to Humans. Non-ionizing radiation, Part 1: Static and extremely low-frequency (ELF) electric and magnetic fields; Monographs on the Evaluation of Carcinogenic Risks to Humans 80, Lyon 2002.
5
European Commission. Possible effects of electromagnetic fields (EMF) on human health, Scientific committee on emerging and newly identified health risks on human health 2006; 1-58.
6
WHO. (World Health Organization) Framework for Developing Health-Based EMF Standards 2006. ISBN 92-4-159433-0.
7
ICNIRP. For limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to 300 GHz). Health Phys 1998; 74(4): 494-522.
8
ICNIRP. On limits of exposure to static magnetic fields. Health Phys 2009; 96(4): 504-14.
9
ICNIRP. On the Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to 300 GHz). Health Phys 2009; 97(3): 257-8.
10
ICNIRP. For limiting exposure to time-varying electric and magnetic fields (1 Hz − 100 kHz). Health Phys 2010; 99(6): 818-36.
11
ICNIRP. For limiting exposure to electric fields induced by movement of the human body in a static magnetic field and by time-varying magnetic fields below 1 Hz. Health Phys 2014; 106(3): 418-25.
12
Calabrò E, Condello S, Currò M, et al. Modulation of HSP response in SH-SY5Y cells following exposure to microwaves of a mobile phone. World J Biol Chem 2012; 3(2): 34-40.
13
Calabrò E, Condello S, Currò M, et al. Effects of low intensity static magnetic field on FTIR spectra and ROS production in SH-SY5Y neuronal-like cells. Bioelectromagnetics 2013; 34(8): 618-29.
14
Calabrò E, Magazù S. Unfolding and aggregation of myoglobin can be induced by three hours exposure to mobile phone microwaves: A FTIR spectroscopy study. Spectroscopy Lett: Int J Rapid Comm 2013; 46(8): 583-9.
15
Calabrò E, Condello S, Currò M, et al. 50 Hz electromagnetic field produced changes in FTIR spectroscopy associated with mitochondrial transmembrane potential reduction in neuronal-like SH-SY5Y cells. Oxid Med Cell Longev 2013; 1-1.
16
Calabrò E, Magazù S. Demicellization of polyethylene oxide in water solution under static magnetic field exposure studied by FTIR spectroscopy. Adv Phys Chem 2013; 1-8.
17
Calabrò E, Magazù S. Unfolding-induced in haemoglobin by exposure to electromagnetic fields: A FTIR spectroscopy study. Orient J Chem 2014; 30(1): 31-5.
18
Calabrò E, Magazù S. Non-thermal effects of microwave oven heating on ground beef meat studied in the mid-infrared region by FTIR spectroscopy. Spectroscopy Lett: Int J Rapid Comm 2014; 47(8): 649-56.
19
Calabrò E, Magazù S. Fourier –self –deconvolution analysis of β-sheet contents in the amide I region of haemoglobin aqueous solutions under exposure to 900 MHz microwaves and bioprotective effectiveness of sugars and salt solutions. Spectroscopy Lett: An Int J Rapid Comm 2015; 48(10): 741-7.
20
Calabrò E, Magazù S. Transition from α-helix to β-sheet structures occurs in myoglobin in deuterium oxide solution under exposure to microwaves (PD 044 29th Annual Symposium of the Protein Society 2015.July 22-25, 2015; Barcelona, Spain. 2015.
21
Calabrò E. Competition between hydrogen bonding and protein aggregation in neuronal-like cells under exposure to 50 Hz magnetic field. Int J Rad Biol 2016; 92(7)(3): 98-403.
22
Calabrò E, Magazù S. Parallel β-sheet vibration band increases with proteins dipole moment under exposure to 1765 MHz microwaves. Bioelectromagnetics 2016; 37(2): 99-107.
23
Calabrò E, Magazù S. Induced-orientation of nitrogen monoxide and azide ion vibrations in human hemoglobin in bidistilled water solution under a static magnetic field. Bioelectromagnetics 2017; 38(6): 447-55.
24
Calabrò E, Magazù S. The α-helix alignment of proteins in water solution toward a high-frequency electromagnetic field: A FTIR spectroscopy study. Electromagn Biol Med 2017; 36(3): 279-88.
25
Pintado T, Maldonado JE. Ultrastructure of platelet aggregation in refractory anemia and myelomonocytic leukemia. I. Ultrastructure of aggregation in normal controls and general defects in refractory anemia and myelomonocytic leukemia. Mayo Clin Proc 1976; 51(6): 379-92.
26
Mattson MP. Calcium and neuronal injury in Alzheimer’s disease. Contributions of beta-amyloid precursor protein mismetabolism, free radicals, and metabolic compromise. Ann N Y Acad Sci 1994; 747: 50-76.
27
Offen D, Elkon H, Melamed E. Apoptosis as a general cell death pathway in neurodegenerative diseases. J Neural Transm Suppl 2000; 58(58): 153-66.
28
Brzyska M, Bacia A, Elbaum D. Oxidative and hydrolytic properties of beta-amyloid. Eur J Biochem 2001; 268(12): 3443-54.
29
Squier TC. Oxidative stress and protein aggregation during biological aging. Exp Gerontol 2001; 36(9): 1539-50.
30
Pogocki D. Alzheimer’s β-amyloid peptide as a source of neurotoxic free radicals: The role of structural effects. Acta Neurobiol Exp (Warsz) 2003; 63(2): 131-45.
31
Chen K, Ballas SK, Hantgan RR, Kim-Shapiro DB. Aggregation of normal and sickle hemoglobin in high concentration phosphate buffer. Biophys J 2004; 87(6): 4113-21.
32
Tripette J, Alexy T, Hardy-Dessources MD, et al. Red blood cell aggregation, aggregate strength and oxygen transport potential of blood are abnormal in both homozygous sickle cell anemia and sickle-hemoglobin C disease. Haematologica 2009; 94(8): 1060-5.
33
Neale RE, Stiller CA, Bunch KJ, Milne E, Mineau GP, Murphy MF. Familial aggregation of childhood and adult cancer in the Utah genealogy. Int J Cancer 2013; 133(12): 2953-60.
34
Magazù S, Calabrò E, Campo S. FTIR spectroscopy studies on the bioprotective effectiveness of trehalose on human hemoglobin aqueous solutions under 50 Hz electromagnetic field exposure. J Phys Chem B 2010; 114(37): 12144-9.
35
Magazù S, Calabrò E. Studying the electromagnetic-induced changes of the secondary structure of bovine serum albumin and the bioprotective effectiveness of trehalose by FTIR spectroscopy. J Phys Chem B 2011; 115(21): 6818-26.
36
Calabrò E, Magazù S, Campo S. Microwave-induced increase of amide I and amide II vibration bands and modulating functions of sodium-chloride, sucrose and trehalose aqueous solutions: The case study of haemoglobin. Res J Chem Environ 2012; 16(4): 59-67.
37
Magazù S, Calabrò E, Campo S, Interdonato S. New insights into bioprotective effectiveness of disaccharides: An FTIR study of human haemoglobin aqueous solutions exposed to static magnetic fields. J Biol Phys 2012; 38(1): 61-74.
38
Magazù S, Calabrò E, Caccamo MT, Cannuli A. The shielding action of disaccharides for typical proteins in aqueous solution against static, 50 Hz and 1800 MHz frequencies electromagnetic fields. Curr Chem Biol 2016; 10(1): 57-64.
39
Calabrò E, Magazù S. Effects of the addition of sodium chloride to a tetrameric protein in water solution during exposure to high frequency electromagnetic field. Open Biotechnol J 2017; 11: 72-80.
40
Fröhlich H. Long range coherence and energy storage in biological systems. Int J Quantum Chem 1968; 2: 641-9.
41
Fröhlich H. Theoretical Physics and Biology 1969; 13.
42
Fröhlich H. Long range coherence and the action of enzymes. Nature 1970; 228(5276): 1093.
43
Fröhlich H. Selective long range dispersion forces between large systems. Phys Lett A 1972; 39(2): 153-4.
44
Fröhlich H. Synergetics 1973; 241-5.
45
Fröhlich H. Evidence for Bose condensation-like excitation of coherent modes in biological systems. Phys Lett A 1975; 51(1): 21-2.
46
Fröhlich H. The extraordinary dielectric properties of biological materials and the action of enzymes. Proc Natl Acad Sci USA 1975; 72(11): 4211-5.
47
Cosic I. The Resonant Recognition Model of Macromolecular Bioactivity: Theory and Applications 1997.
48
Cosic I, Cosic D, Lazar K. Is it possible to predict electromagnetic resonances in proteins, DNA and RNA? EPJ Nonlinear Biomed Phy 2015; 3: 5.
49
Becker L, Bannwarth M, Meisinger C, et al. Preprotein translocase of the outer mitochondrial membrane: Reconstituted Tom 40 forms a characteristic TOM pore. J Mol Biol 2005; 353(5): 1011-20.
50
Villinger S, Briones R, Giller K, et al. Functional dynamics in the voltage-dependent anion channel. Proc Natl Acad Sci USA 2010; 107(52): 22546-51.
51
Szabo I, Zoratti M. Mitochondrial channels: Ion fluxes and more. Physiol Rev 2014; 94(2): 519-608.
52
Preto J, Pettini M. Resonant long-range interactions between polar macromolecules. Phys Lett A 2013; 377(8): 587-91.
53
Grundler W, Keilman F. Sharp resonances in yeast growth from non-thermal sensitivity to microwaves. Phys Rev Lett 1983; 51: 1214-6.
54
Edwards GS, Davis CC, Saffer JD, Swicord ML. Resonant absorption of DNA molecules. Phys Rev Lett 1984; 53: 1284-7.
55
Adair RK. Effects of weak high-frequency electromagnetic fields on biological systems.Radiofrequency Radiation Standards 1995; 207-22.
56
Stewart W. Mobile Phones and Health, Independent Expert Group on Mobile Phones 2000.
57
Lin JC. Mechanisms of field coupling into biological systems at ELF and RF frequencies. Advances in electromagnetic fields in living systems 2000; 3: 1-38.
58
Michaelkson SM, Lin JC. Biological effects and health implications of radio frequency radiation 1987.
59
Calabrò E, Magazù S. Experimental verification of the far-field approximation for a mobile phone antenna. J Electromagn Waves Appl 2017; 31(14): 1421-33.
60
Adair RK. Biophysics limits on the biological effects of ultrawide band electromagnetic radiation 2000.
61
Calabrò E, Magazù S. Direct spectroscopic evidence for competition between thermal molecular agitation and magnetic field in a tetrameric protein in aqueous solution. Phys Lett A 2018; 382: 1389-94.
62
Adair RK. Vibrational resonances in biological systems at microwave frequencies. Biophys J 2002; 82(3): 1147-52.
63
Belyaev IY, Alipov YD, Polunin VA, Shcheglov VS. Evidence for dependence of resonant frequency of millimeter wave interaction with Escherichia coli k12 cells on haploid genome length. Electro Magnetobiol 1993; 12(1): 39-49.
64
Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 1952; 117(4): 500-44.
65
Ashcroft FM, Ed. Ion Channels and Disease 2000.
66
Blackiston DJ, McLaughlin KA, Levin M. Bioelectric controls of cell proliferation: Ion channels, membrane voltage and the cell cycle. Cell Cycle 2009; 8(21): 3527-36.
67
Huang X, Jan LY. Targeting potassium channels in cancer. J Cell Biol 2014; 206(2): 151-62.
68
Miles AJ, Wallace BA. Circular dichroism spectroscopy of membrane proteins. Chem Soc Rev 2016; 45(18): 4859-72.
69
Nguyen KT, Le Clair SV, Ye S, Chen Z. Orientation determination of protein helical secondary structures using linear and nonlinear vibrational spectroscopy. J Phys Chem B 2009; 113(36): 12169-80.
70
Woody RW, Tinoco I. Optical rotation of oriented helices. III. Calculation of the rotatory dispersion and circular dichroism of the Alpha and 310Helix. J Chem Phys 1967; 46: 4927-45.
71
Ulmschneider MB, Sansom MSP, Di Nola A. Evaluating tilt angles of membrane-associated helices: Comparison of computational and NMR techniques. Biophys J 2006; 90(5): 1650-60.
72
Holt A, Koehorst RBM, Rutters-Meijneke T, et al. Tilt and rotation angles of a transmembrane model peptide as studied by fluorescence spectroscopy. Biophys J 2009; 97(8): 2258-66.
73
Stech EI, Payne PR. Dynamic Models of the Human Body NASA – Aerospace Medical Research Laboratory Defense Documentation Center 1969; 22314.
74
Ethier CR, Simmons CA. Introductory Biomechanics – From Cells to Organisms 2007.
75
Escalante-Marinez JE, Gomez-Aguilar JF, Calderon-Ramon C, Morales-Mendoza LJ, Cruz-Orduna I, Laguna-Camacho JR. Experimental evaluation of viscous damping coefficient in the fractional underdamped oscillator. Adv Mech Eng 2016; 8(4): 1-12.
76
Zerbato D, Galvan S, Fiorini P. Calibration of mass spring models for organ simulations. Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems 2007.San Diego. 2007.USA. 2007.
77
Dokos S. Modelling organs, tissues, cells and devices using Matlab and Comsol Multiphysics 2017.