All published articles of this journal are available on ScienceDirect.
Mathematical Model of Human Forearm Based Muscle Fiber Tissues’ Anisotropic Characteristics
Abstract
On the basis of human muscle fiber tissues' characteristics, it is first proposed to establish the analytical model of galvanic coupling intra-body communication channel. In this model, the parallel and the transverse electrical characteristics of muscular tissue are fully considered, and the model accurately presents the transmission mechanism of galvanic coupling intra-body communication signals in the channel.
INTRODUCTION
The galvanic coupling intra-body communication is a newly-developing short-distance wireless communication mode, with human tissues as the signal transmission media [1, 2]. Because signals are transmitted directly through these tissues, their characteristics will produce a direct effect on the attenuation characteristic of the channel. Muscular tissues are an important part of human body, which is developed from muscle fiber with the parallel and the transverse growth characteristics [3]. In the conventional volume conductor analytical model, the frequently-used way is to consider the muscular layer and other layers to be isotropic [1, 2]. This way cannot show electrical characteristics of muscle fiber effectively, but the physical property of the model is changed, and model precision is lowered. In this paper, on the basis of the transformational relation of muscle fiber’s anisotropy and tissue’s isotropy in the cylindrical coordinate, the analytical model of the intra-body communication channel based on human forearm surface is established and verified.
METHODS
The length of human forearm is assumed to be h and equivalent to a multilayer volume conductor cylinder model comprised of skeleton, muscle, fat and skin, (r1,r2,..rn) represents circumscribed radiuses of all tissues on the tangent plane (εt1,εt2,..εtn), and (εl1,εl2,..εln) represent the transverse and the parallel permittivity’s of all tissues respectively, (δt1,δt2,..δtn) and (δl1,δl2,..δln) indicate the transverse and the parallel electric conductivity of all tissues (shown in (Fig. 1)), respectively. In the galvanic coupling intra-body communication, when the electrical signal’s frequency in the input electrode is less than 1MHz [1, 4], the propagation effect, the inductive effect and the irradiation effect from the skin to air throughout the channel may be basically ignored. As the frequency is increased, the capacitance effect of the tissue becomes more and more obvious; therefore its impact on the overall system shall be taken into account in building the tissue model. The abbreviated equation [5] of the tissue’s potential distribution can be approximately derived in the cylindrical coordinate system by means of Maxwell’s equation under the quasi static approximation condition [1, 2, 5]:
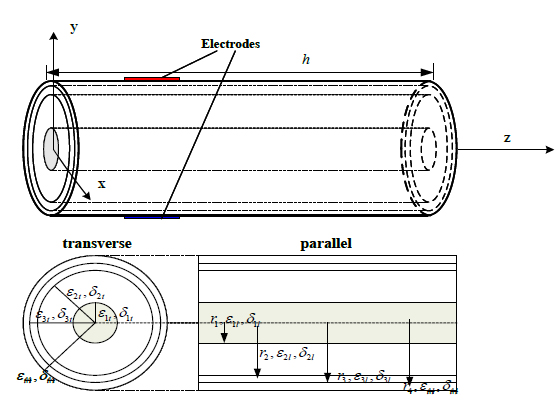
Equivalent multi-layer cylindrical model of human arm.
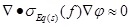
|
(1) |
Where  represents the interior electric potential in the tissue of human forearm, σEQ(s)(f) indicates the combination conductivity of the tissue in the S-th layer at the frequency of f and its expression is as follows:
represents the interior electric potential in the tissue of human forearm, σEQ(s)(f) indicates the combination conductivity of the tissue in the S-th layer at the frequency of f and its expression is as follows:
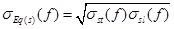
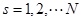
|
(2) |
Where σst (f) and σsl (f) represent respectively the tangential composite electric conductivity and the lateral one of the tissue in the S-th layer at the frequency of f, they are expressed as follows:
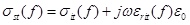
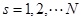 , ,
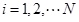
|
(3) |
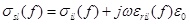
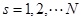 , ,
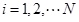
|
(4) |
where σit (f) and σil (f) indicate the transverse and the parallel conductivity of the tissue in the i-th layer at the frequency of f respectively, εrit (f) and εrit (f) indicate the transverse and the parallel relative permittivity of the tissue in the i-th layerat the frequency of f, respectively, and ε 0 represents the permittivity in the vacuum. On the basis of the cylindrical coordinate transformation relation between muscle fiber’s anisotropy and tissues' isotropy, the following can be derived [6]:
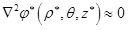 |
(5) |
And
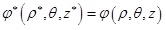 |
(6) |
Where
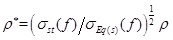 and
and
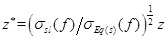 .
.
Channel Model with Muscle Fiber Characteristics
In combination with quasi-static approximation electromagnetic boundary conditions and Laplace’s equation of the anisotropic tissue in the cylindrical coordinate system, the variable separation approach is used to derive electric potential distribution of all layers of human forearm’ tissues at the frequency of f, which may be expressed as follows:
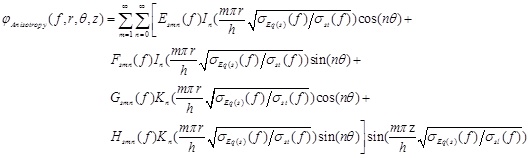 |
(7) |
S = 1,2...N
where In(●) is the n-order modified Bessel function of the first kind, Kn(●) is the n-order modified Bessel function of the second kind; Esmn (f), Fsmn(f), Gsmn (f) and Hsmn (f) indicate constant coefficients of the electric potential equation concerning the tissue in the S-th layer at the frequency of f, respectively.
Isotropic Channel Model
When
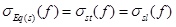 is true, it means that the tissue’ characteristics in all directions are identical at the frequency of f, so the electric potential equation of the isotropic tissue in the cylindrical coordinate system can be obtained as follows:
is true, it means that the tissue’ characteristics in all directions are identical at the frequency of f, so the electric potential equation of the isotropic tissue in the cylindrical coordinate system can be obtained as follows:
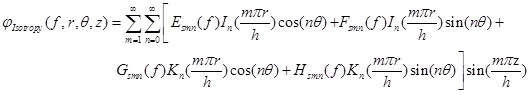 |
(8) |
S= 1,2...N
Experiment parameters.
| Position | Perimeter of source position | Perimeter of detected position | Average outside diameter | Communication distance |
|---|---|---|---|---|
| Arm | 29.5cm | 25cm | 4.335cm | 6cm |
Calculation and Verification
In order to verify reasonability of the model effectively, the preliminary confirmatory experiment is carried out. We select healthy volunteers to perform this confirmatory experiment (see Table 1) for their arm testing parameters; the experiment is performed between shoulder joint and elbow joint). In the experiment, we use AgCl electrodes with the size of 4cm*4cm as the signal electrode and the signal acquisition electrode; 1 mA current is input through the signal electrode. When human body remains stationary, averaging multiple measured values is used as the experimental result of the sample; from Reference [1], it can obtain electrical parameters of the isotropic model and the anisotropic model, and the electrical parameters are put in the model so as to derive the attenuation index of the channel. The experimental result and the computed result are shown in Fig. (2).
In the experiment, a network analyzer (4395A, Agilent Technologies, Santa Clara, California, USA) and a differential probe (1141A, Agilent Technologies, Santa Clara, California, USA; 1142A, Agilent Technologies, Santa Clara, California, USA) were used. The network analyzer was used to measure the signal attenuation from the implanted devices to the surface electrodes and the differential probe was used to break the common ground loop between the transmitted port and the received port of the network analyzer.
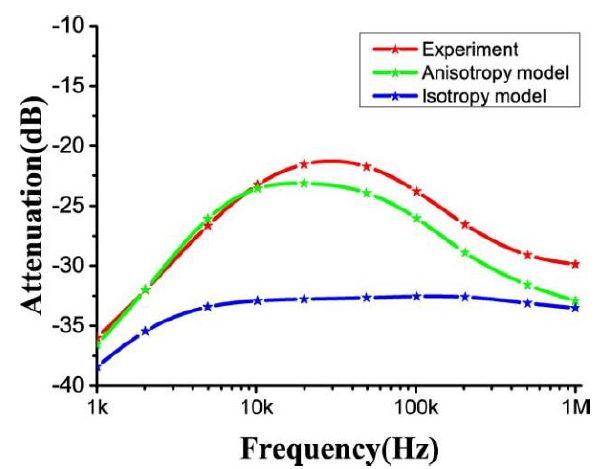
Computed result and experimental result of the model.
It can be found from Fig. (2) that, in the anisotropic channel model, when the frequency lies within the range of 1kHz to 10kHz, channel attenuation is reduced as the frequency rises; channel attenuation tendency becomes relatively steady as the frequency grows within the frequency range of 10kHz to 50kHz; while channel attenuation is increased as the frequency is raised within the frequency range of 50kHz to 1MHz; these properties are basically identical with the experimental results. For the isotropic channel model, it’s computed result conforms to the experimental result at the frequency less than 20 kHz, however, when the communication frequency exceeds 20 kHz, attenuation of the isotropic model is hardly changed, this is significantly different from the experimental result. It is important that, within the frequency range, the average error of the channel model with muscle fiber characteristics is reduced by 21% compared with that of the channel model without these characteristics. This improves the precision of the model further.
CONCLUSION
In this model, tissue characteristics of muscle fiber are adequately considered. By comparing the computed result of the channel model with muscle fiber characteristics, the computed result and the experimental result of the isotropic channel model, it is found that the computed result and the experimental result of the channel model with muscle fiber characteristics are almost the same; the maximum error of the model is 10% and the average error is 5.97% within the frequency range. Compared with the simplified isotropic model, the average error is lowered by 21%, so the model precision is greatly enhanced.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This work presented in this paper is supported by The Key Fund Project of Sichuan Provincial Department of Education under Grant13ZA0003, Grant 14ZB0360, Grant 14ZB0363 , Grant 14ZB0352; The Sichuan Province Department of Science and Technology under Grant 2015JY0119, the Key Fund Project of Leshan Science and Technology Bureau (15ZDYJ0177).


