All published articles of this journal are available on ScienceDirect.
Bioremediation of Waters Polluted by Endocrine Disruptors by Means of the Process of Thermodialysis
Abstract
The advantages in using catalytic hydrophobic membranes in bioreactors operating under non-isothermal conditions, process of thermodialysis, for remediation of aqueous systems polluted by Endocrine Disruptors are discussed and illustrated. In presence of a transmembrane temperature gradient the enzyme activity increases along the yield of the bioremediation process. The theoretical bases accounting for the enzyme activity increase are highlighted and results supporting the theoretical approach are shown. An overview of the catalytic systems used towards different Endocrine Disruptors is listed.
1. INTRODUCTION
Endocrine Disruptors Chemicals (EDCs) are compounds, synthetic or natural, so called for their ability of interacting with the endocrine system thus inducing severe pathologies not only in exposed wildlife and humans, but also in their progeny. EDCs have been proved to induce cancer [1], to damage the male and female reproductive system [2-4], to induce obesity [5, 6] and cardiovascular diseases [7, 8]. A great number of compounds have been identified as belonging to this group of chemicals: natural and synthetic steroid hormones, phytoestrogens, alkylphenols, phthalates, pesticides, surfactants and polychlorinated biphenyls. Among the EDCs Bisphenol A (BPA) is one of the most abundant in the environment and the most studied.
Endocrine Disruptors reach the humans mainly through the food, but their presence is widespread in aqueous systems, particular in superficial waters, where they put severe risks for the preservation of the biodiversity of the species there living. Concerning BPA it enters into the environment mainly from the discharges of industrial wastewater treatment plants (WWTPs), leachates of waste plastic in landfills, processing of BPA in manufactures, and spray paints.
Due to their retention and harmful effects, the fate of EDCs in the environment has become a social issue by the public community and the need of removing them from the aquatic ecosystems is an imperative.
Many physico-chemical and biotechnological methods have been used to this aim.
Physico-chemical methods include photodegradation [9], oxidation [10, 11], absorption on active carbon [12, 13] and classical membrane processes such as ultrafiltration and nanofiltration [14, 15].
Biotechnological methods are pursued by means of enzymes [16, 17], by whole microbial cells in suspension or grown as biofilm [18-20], by phytoremediation [21, 22]. These last biotechnological processes are recognized as bioremediation.
Enzyme bioremediation has been proved to be the most appropriate since it selectively reduces the concentration of the harmful compound, remaining unchanged those of the other compounds.
In bioremediation processes with enzymes usually the biocatalyst is used immobilized. Immobilized enzymes offer many advantages in respect to their free counterpart. Among the advantages we recall higher resistance to extreme values of temperature and pH, major time stability and, more interesting from the industrial point of view, the possibility of reuse. The best way to immobilize the enzyme is the covalent bond to a solid carrier, for example beads, jell or membranes. Enzyme immobilization on a membrane made us to think on the possibility of applying to the catalytic composite system the process of Thermodialysis, discovered and patented by us many years ago [23] as “Process of thermal diffusion across porous partitions and relative apparatuses”.
Under the name of Thermodialysis is known the process by which the components of a solution are selectively fractionated across a hydrophobic, porous and uncharged solid membrane separating two solutions, of equal or different composition, kept at different temperatures. Under these conditions the membrane per se “unselective” becomes “selective”. The driving force of the process, according to the classical approach of the Thermodynamics of Irreversible Processes [24, 25], is the temperature gradient which, in Gaeta’s theory [26], produces differential forces on the solute and solvent molecules. From this point of view the solution in the membrane pores can be considered a microscopic Soret cell [27] where a modified thermal diffusion occurs.
The employment of catalytic hydrophobic porous membranes in bioreactors operating in the presence of a temperature gradient has been patented by us since 1992 [28]. The rationale for this process is illustrated in section 2.
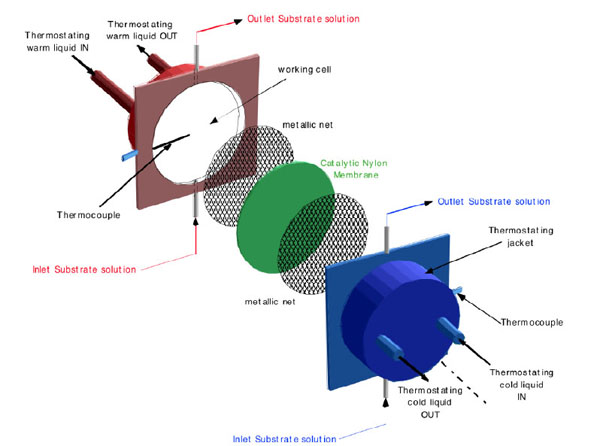
Schematic representation, of the non-isothermal membrane bioreactor.
2. RATIONALE
In Figs. (1 and 2a) schematic pictures of the non-isothermal bioreactor are represented. The bioreactor consists of two metallic flanges in each of which a shallow cylindrical cavity is bored, 70 mm in diameter and 2.5 mm in depth. Each half-cell, so built, constitutes the working volume filled with the aqueous solution to be treated. The catalytic membrane is clamped between the two flanges in order to separate and, simultaneously, to connect the solutions filling the half-cells. Solutions are circulated in each half-cell by means of two peristaltic pumps through hydraulic circuits starting and ending in the same reservoir. In this way the only changes in the solution are those relative to the substrate interacting with the immobilized enzyme. Using independent thermostats, the half-cells are maintained at predetermined temperatures. Thermocouples placed 1.5 mm away from the membrane surfaces measure the local temperature of the solution in each half-cell, i.e. T(w) (warm temperature) and T(c) (cold temperature). These measurements allow calculating the real temperature profile across the catalytic membrane, being laminar the solution motion in each half-cell and being the Reynolds number lower than Re critical [29]. Consequently the heat propagation in the bioreactor occurs by conduction between isothermal liquid planes perpendicular to the direction of the heat flow. In this case, if the thermal conductivity and thickness of both filling solutions and membrane are known, it is possible to calculate the temperatures on the membrane surfaces by applying the heat flux continuity principle. In (Fig. 2b) the situation corresponding to T(w)= 40 °C and T(c) = 20°C is represented, while T*(w) and T*(c) indicate the effective temperatures on the two sides of the catalytic membrane. It has been found that ΔT*= (T*(w)- T*(c)) = β ΔT = β (T(w) – T(c)), where β for the membranes employed by us (Teflon or Nylon) has been calculated to be about 0.1.

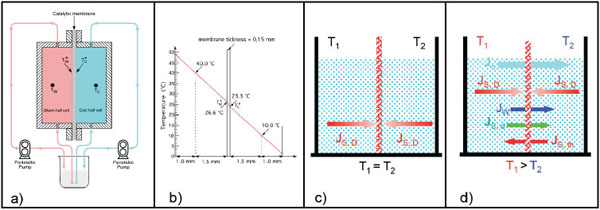
(a) Modus operandi of the non-isothermal membrane bioreactor; (b) Temperature profile across the non-isothermal membrane bioreactor; (c) Diffusive substrate fluxes when the membrane bioreactor operates under isothermal conditions; (d) Heat flux and matter assosiated fluxes in a non-isothermal membrane bioreactor.
In Fig. (2) the modus operandi of an enzyme immobilized on a hydrophobic and porous membrane employed in an isothermal Fig. (2c) or non-isothermal Fig. (2d) bioreactor is also illustrated. Under isothermal conditions the enzyme interacts with the substrate molecule only by diffusion according to the Fick law. Under non-isothermal conditions the catalytic membrane, in addition to the heath flow, is crossed by the matter fluxes indicated in Fig. (2d), i.e. by: i) a massive water flux, Jw, driven by the thermodialysis process and proceeding from the warm to the cold half-cell; ii) a substrate flux, Js,d, known as solute drag and associated to the water flux; and iii) a further substrate flux, Js,th, driven by the temperature gradient. The analytical expressions for each of these fluxes are reported in Box 1 where it is possible to see how they are proportional to the applied temperature gradient ΔT*/Δx (or ΔT/Δx). Of course the diffusive substrate fluxes, JD, still remain. Consequently in presence of a temperature gradient the immobilized enzymes encounter, in the unit of time, more substrate molecules that in absence of a temperature gradient. Since the reaction rate is determined by the number of substrate molecules interacting in the unit of time with the catalytic sites on the membrane it follows that under non-isothermal conditions the reaction rate increases proportionally to the size of the temperature gradient applied across the membrane. In addition the massive water flow, Jw, produced by the process of thermodialysis, plays a synergetic role in favor of the reaction rate by removing from the catalytic sites the reaction product/s, so allowing the enzyme to perform more reactions in the unit of time. In other words the non-isothermal conditions increase the turnover number of the reaction proportionally to the applied transmembrane temperature gradients.
3. PHENOMENOLOGY OF A CATALYTIC PROCESS MEDIATED BY THE PROCESS OF THERMODIALYSIS
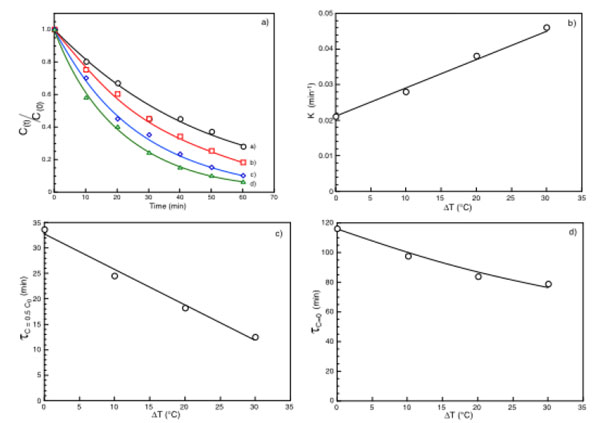
(a) Normalized substrate concentration as a function of time under ΔT = 0°C (○), ΔT = 10 °C (□), ΔT = 20 °C = (◊), ΔT = 30 °C (Δ); (b) k values as a function of the applied ΔT; (c) (τc=0.5co) as a function of the applied ΔT; (d) τc=0 as a function of the applied ΔT.
To introduce the experimental part we firstly report the typical phenomenology of how the experimental results are handled.
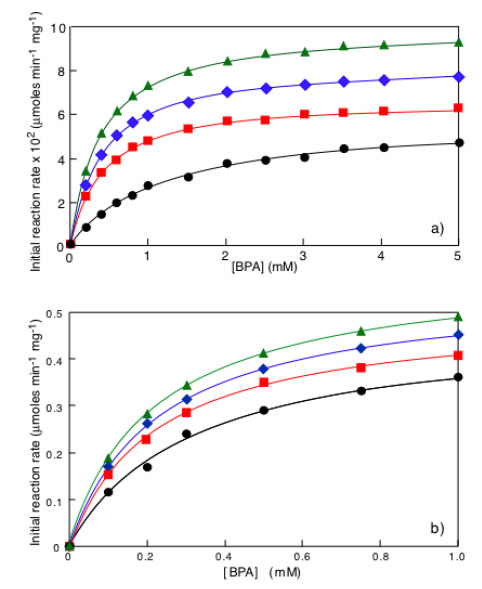
In Fig. (3a) the typical time dependence of an enzymatic removal of a pollutant under isothermal and non-isothermal conditions is shown. Each curve is fitted by a general equation of the type:
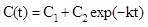
where C(t) is the pollutant concentration existing at time t, C1+ C2 = C0, i.e. the initial pollutant concentration, C1 is the asymptotic steady state pollutant concentration in the case of enzyme inhibition by the reaction product. In absence of product inhibition C1 = 0 and C2 = C0 and equation 1 becomes:
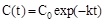
In both equations k, measured in time-1, is a time constant indicative of the rate of substrate removal. k depends from the nature and concentration of the substrate, from the isothermal or non-isothermal conditions. Interesting enough the plot of the k values as a function of ΔT (or ΔT*), at fixed pollutant concentration, exhibits Fig. (3b) a linear dependence increasing with the increase of ΔT. Other interesting parameters that can be derived by the results in Fig. (3a) and from equations 1 or 2 are the times requested to halve (τc=0.5co) or to eliminate (τc=0) the initial pollutant concentration. Both parameters Fig. (3c and d) decrease with the increase of the applied ΔT, confirming that under non-isothermal conditions the enzyme reaction rate is greater in respect to that of the isothermal conditions. These results can be attributed exclusively to the process of thermodialysis. Indeed in the absence of any flux driven by the temperature gradient and considering only the temperature dependence of the enzyme activity, the small temperature difference across the membrane faces suggests that what is gained on the warm surface of the catalytic membrane it is exactly lost on its cold face.
Initial reaction rate as a function of BPA concentration in the case of immobilized laccase (a) or immobilized tyrosinase (b). Symbols: ΔT = 0°C (●), ΔT = 10 °C (□;), ΔT = 20 °C = (◊), ΔT = 30 °C (Δ). Adapted from reference [30].
4. ACTUAL RESULTS
From curves similar to those reported in Fig. (3a) it is possible to derive the initial enzyme reaction rate, expressed in moles/min/mg of enzyme, by multiplying the value of the tangent to the curve of c(t) as a function of time in the initial part, i.e. the value of Δc/Δt for Δ approaching to zero, for the volume of treated solution. Following this approach one obtains the actual results reported in Fig. (4) showing, as a function of BPA concentration, the initial reaction rates under isothermal and non-isothermal conditions when laccase Fig. (4a) or tyrosinase Fig. (4b) were covalently immobilized on a hydrophobic nylon membrane (Hydrolon from Pall), chemically grafted with glycidyl methacrylate. Detailed description of technologies used for membrane activation and enzyme immobilization can be found in reference [30].
Results in Fig. (4a and b) show: i) a Michaelis-Menten behavior either under isothermal or under non-isothermal conditions; ii) at each BPA concentration the initial enzyme reaction rate under non-isothermal conditions is greater than the one under isothermal conditions.
By plotting as a function of the applied ΔT or ΔT* the values of the initial reaction rate at each concentration one obtains the results of Fig. (5) where the cases of BPA concentrations equal to 0.4 mM(o) and to 4 mM(☐) are reported. Results refer to the treatment with laccase. The same occurs for all the concentrations explored and also when the results relative to the tyrosinase are considered. Being linear the dependence between the initial reaction rate and the ΔT, one can write:
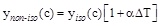
where ynon-iso(C) and ynano-iso(C) are the values of the initial reaction rate under non-isothermal and isothermal conditions at the pollutant concentration (c) and α represents the Percentage Activity Increase (P.A.I.) of the initial enzyme activity when the temperature difference between the thermocouples position is 1°C. The expression for α is:
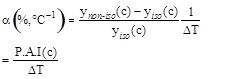
When the actual temperature difference ΔT* across the two membrane surfaces is considered, one obtains:
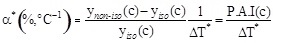
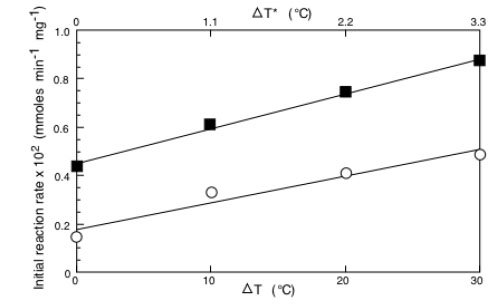
Initial reaction rate of immobilized laccase as a function of ΔT (or ΔT*) as a function of BPA concentration equal to 0.4 (o) or 4.0 mM (□). Adapted from reference [30].
where α* is the percentage activity increase when the transmembrane ΔT* is equal to 1. Considering the expressions (4) and (5) one obtains:
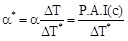
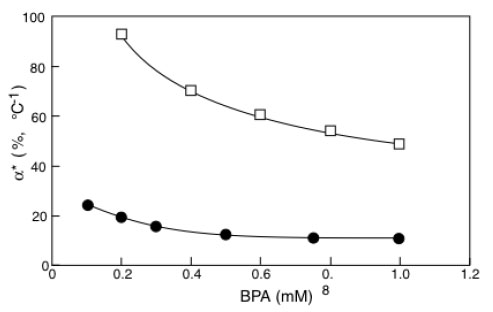
α*values for immobilized laccase (□) or tyrosinase (●) as a function of BPA concentration. Adapted from reference [30].
In Fig. (6) the α* values obtained by elaborating the results in Fig. (4a and b) have been reported as a function of BPA concentration. It is interesting to observe that the percentage activity increases (the α* are proportional to P.A.I.) induced by the temperature difference on laccase activity are about five times higher than those induced on tyrosinase. Calculations have been reported only for the common BPA concentration range explored with laccase and tyrosinase.
5. PRACTICAL CONSIDERATIONS
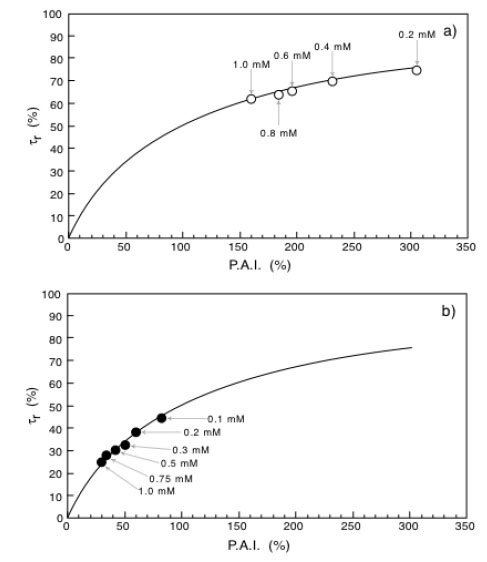
Bioremediation reduction times as a function of Percentage Activity Increase (P.A.I.) for immobilized laccase (a) or immobilized tyrosinase (b). Adapted from reference [30].
All the results above reported clearly indicate that: i) it is possible to bioremediate aqueous systems polluted by BPA by using immobilized laccase or tyrosinase; ii) the bioremediation efficiency increases when the immobilized catalyst operates under non-isothermal conditions; iii) under non-isothermal conditions laccase results more efficient than tyrosinase.
To better quantify the effect of the transmembrane temperature gradient it is interesting to correlate, at each BPA concentration, the α* value with the reduction of the bioremediation time, τr, defined as
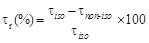
where τnon-iso and τiso are the times required to obtain the same percentage of pollutant removal under non isothermal and isothermal conditions, respectively. The same value of BPA removal, i.e. the same value of BPA concentration under non-isothermal (cnon- iso) and isothermal (ciso) conditions is reached, when:
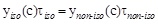
Remembering equation 2, one can write:
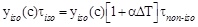
by which, taking in account equation (1) and equation (2) one obtains:
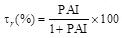
Equation 10 is similar to that of an equilateral iperbola whose generic plot of τr as a function of P.A.I. is represented by the continuous line reported in Fig. (7a and b). Looking at these figures it is also possible to appreciate how the experimental points obtained with the immobilized laccase (Fig. 7a) or tyrosinase Fig. (7b) exactly fit with the theoretical curve. The indication coming out from (Fig. 7) is that the reduction of the bioremediation times is function of the percentage increase of the enzyme activity (P.A.I.) and therefore of the temperature difference applied across the catalytic membrane. This is a clear demonstration of the effectiveness of the thermodialysis process on the activity of an enzyme immobilized on hydrophobic porous membranes. A confirmation of this conclusion comes out from the results of Fig. (8) where the reduction of bioremediation times is reported as a function of the BPA concentration. Interesting enough the reduction of the bioremediation times decreases with the increase of BPA concentration. This result is expected by considering that when an enzyme works at high substrate concentrations the additional substrate fluxes driven by the thermodialysis process are less effective than those occurring at low concentrations.
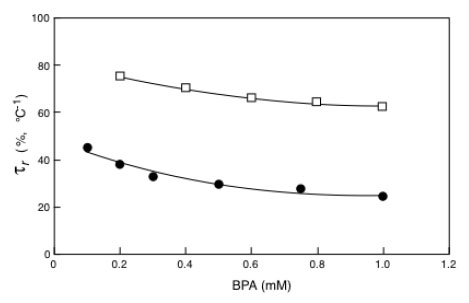
Bioremediation reduction times as a function of BPA concentration for immobilized laccase (□) or immobilized tyrosinase (●). Experimental conditions: Tav = 20 °C and DT 0 30°C. Adapted from reference [30].
All together these results are important from the ecological point of view since in the present case mM concentrations have been used, while those existing in nature (in superficial and deep waters as well as in biological fluids) are of the order of nM.
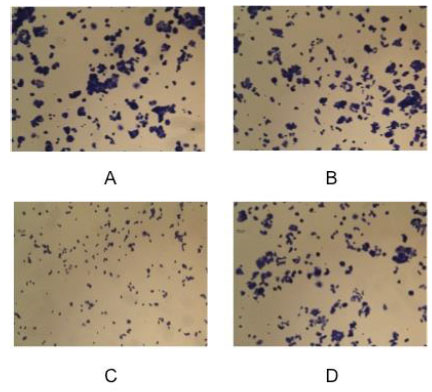
Inverted microscope images showing the effect of bioremediation on MCF-7 cells growth after 48 hour of incubation: (A) control, (B) vehicle, (C) pre-bioremediation, (D) post-bioremediation.
At this point the biologist has a question: the clean-up is real? From the chemistry point of view the bioremediation is complete when the pollutant concentration becomes zero, but this is not completely true for a biologist particularly when the pollutant is an endocrine disruptor insomuch the reaction products can exhibit estrogenic activity more powerful than its parent. To solve this question we have measured the proliferation of MCF-7 cell in presence of the same BPA solution enzyme treated or untreated. The initial BPA concentration was 0.2 mM and the enzyme treatment lasted 36 h. Of course negative and positive controls were used. The crystal violet assay was employed. The results of this investigation are reported in Fig. (9). Cells were grown in a multiwell for 48 h. Panel A is a picture of the natural cell growth, panel B represents the cell growth with the buffer employed in the bioreactor during the enzyme reaction, panel C represents the cell grown in presence of untreated BPA solution, Panel D indicates the cell grown in presence of the initial BPA solution enzyme treated for 36 h. A simple inspection to the figures shows that the cell growth under condition C is strongly inhibited for toxicity compared to panel A and B, while panel D shows the same cell growth than in panels A and B.
In Fig. (10) the results of Fig. (9) are reported as optical densities after the assay with the crystal violet method.
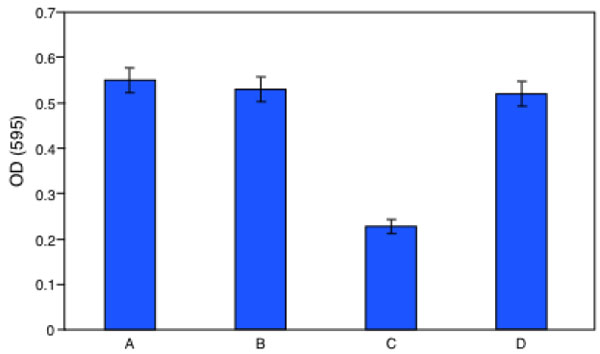
Crystal Violet assay: Measure, as optical density at 595 nm, of MCF7 cells proliferation after 48 hour of incubation: (A) control, (B) vehicle, (C) prebioremediation, (D) postbioremediation.
Some catalityc systems employed in non-isothermal membrane bioreactors after 2000.
| Enzyme | Substrate | Membrane | Membrane Activation | Material Grafted | Spacers and Coupling Agent | Reference |
|---|---|---|---|---|---|---|
| β-galactosidase from Aspergillus Oryzae |
Lactose | teflon | γ-radiation | MAA and HEMA | HMDA and GA | [31] |
| Penicillin G acylase from E. Coli |
Cephalexin | nylon | γ-radiation | MMA | HMDA and GA | [32] |
| β-galactosidase from Aspergillus Oryzae |
Lactose | nylon | Chemical | MAA | HMDA and GA | [33] |
| β-galactosidase from Aspergillus Oryzae |
Lactose | nylon | Chemical | Sty-MAA | HMDA and GA | [33] |
| β-galactosidase from Aspergillus Oryzae |
Lactose | nylon | Chemical | BMA | HMDA and GA | [34] |
| β-galactosidase from Aspergillus Oryzae |
Lactose | nylon | Chemical | BMA | HMDA and GA | [35] |
| Urease | Urea | nylon | Ghemical | BMA | HMDA and GA | [36] |
| Penicillin G acylase from E. Coli |
Cephalexin | nylon | Chemical + γ radiation |
MMA | HMDA and GA | [37] |
| β-galactosidase from Aspergillus Oryzae |
Glucose | nylon | Chemical | BMA at different concentrations |
HMDA and GA | [38] |
| β-galactosidase from Aspergillus Oryzae |
Glucose | nylon | Chemical | GMA | PDA and diazotization |
[39] |
| β-galactosidase from Aspergillus Oryzae |
Glucose | nylon | Chemical | GMA | PDA and condensation |
[39] |
| Penicillin G acylase from E. Coli |
PGME and 7-ADCA | nylon | Chemical | BMA | HMDA and GA | [40] |
| Urease from Jack beans | urea | nylon | Chemical | MMA | HMDA or HZ with GA |
[41] |
| β-galactosidase from Aspergillus Oryzae |
lactose | Nylon | Chemical | GMA | [HMDA or HTDA or HZ] + GA |
[42] |
| Urease from Jack beans | urea | nylon | Chemical | CHMA | HDMA and GA | [43] |
| Laccase from Rhus Vernicifera |
Quinol | nylon | Chemical | GMA | HMDA | [44] |
| β-galactosidase from Aspergillus Oryzae |
Milk | Polypropylene hollow fibers |
Chemical | HMDA | HMDA and GA | [45] |
| Laccase from Trametes Versicolor | Syringic acid | nylon | Chemical | GMA | PDA | [46] |
| Laccase from Trametes Versicolor |
BPA | nylon | Chemical | GMA | PDA | [47] |
| Laccase from Rhus Vernicifera |
Phenol | Polypropylene | Chemical with cromic acid |
none | EDA and GA | [48] |
| Acetylcholinesterase | Acetylcholine iodide | PAN membranes | Chemical | EDA | With or without chitosan | [49] |
| Lipase from Candida Rugosa |
Dimethylphthalate | Polypropylene | Plasma reactor | Acrylic Acid and He |
PDA | [50] |
At this point, to give an idea of all the work done by us using our patented process, a list of the different catalytic systems used in the last years is reported in Table 1.
Summing up it is possible to conclude that the bioremediation process carried out by means of enzymes immobilized on hydrophobic porous membranes operating in non-isothermal bioreactors is more advantageous in respect to the same catalytic membrane operating in isothermal bioreactors.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
We thank the Interuniversity Consortium INBB for financing with post-doc fellowship Dr. M. Forte and Dr. L. Mita.


